Welcome to another tutorial, here you will learn about Numbers and various Math functions available in python language.
In handling numbers, you will learn the commonly used math operators and how you can use them to perform various operations in python. You will also, learn about shortcuts referred to as functions, which help calculate some of the complex mathematical expressions such as sine/cosine, factorials, power, and so on.
As we begin, I’ll recommend you leave your IDLE open as you are reading the instructions here; so you can practice simultaneously.
There 6 basic mathematical operators in Python.
You must be familiar with most of the operators mentioned above apart from the modulo operator. In the course of this tutorial, you will learn how the modulo operator works.
This is simply the addition of numbers. Now, let’s see how this actually works, so open your IDLE and type a number, then add the + sign and add another number to the first one, then hit the enter key. Check the example below:
>>> 10+11
21Once the enter key is pressed, the answer will appear below the written code.
You can try out more examples with different numbers and the addition operator.
Its operation is quite similar to addition in terms of syntax. All you need to do is to use the – sign and with any random number. Check out the example below:
Example: We used 89.33 and 23.67, which gave the output of 65.55.

For this operator, you will use the * ( also known as asterisk). So you can try it out. Check out the example below.

For this operator, the / sign is used. You can use it with any set of random numbers. Check out the example below to better understand how this works.
>>> 16/2
8Let’s try another set of numbers say 15 and 2. What do you think the answer will be? In mathematics, the answer should be 7.5, however, when this is tried in the IDLE, the compiler will return 7 as the answer. This is because if any operation performs on an integer, then the answer would be an integer. Just like in the example here, 15 and 2 are integers and the answer returned is 7, which is an integer. The reason why it turned out to be 7 instead of another number is that the answer is determined as the closest smaller integer to the original answer. The original answer in the example is 7.5 and the nearest integer to it is 7 and 8, but we have to pick the smaller one which is 7. This attribute is known as floor function. This is in Python.
Check out the example below for more clarification.

However, Python is the known programming language that has this type of operator. Other languages make use of pre-defined functions (or shortcuts as mentioned earlier) to compute this. Now, to make use of the operator, use two asterisks (i.e. **) between any two numbers. Check out the example below:
>>> 2**10
1024At this stage, it is time for you to combine multiple operators and make use of them. It is advisable to use brackets, as this will help Python to understand what you want as the answer. For instance, rather than writing 2-9.0/2, write 2 – (9.0/2). This goes with the normal BODMAS, how it is used to solve mathematical expressions with multiple operators.

For this operator, the ‘%’ (percentage) sign is used. In Modulo operator, if used with two operands, returns the remainder as the answer. Check out the example below:
12%2 = 0, since 2 perfectly divides .
13%2 = 1, since dividing 13 with 2 leaves 1 as remainder.
19%5 = 4, because, again, 19/5 leaves 4 as the remainder.
It is also explained in the example below:

This is the end of the number operators, let's continue the next session with the math function.
In your course of study as a python programmer, it might be necessary for you to create a scientific calculator for a project or something else. There might need for you to evaluate complex mathematical operations, such as trigonometric operations, logarithmic operations, and so on. Aside from developing a calculator, you can face other situations where you need to use these functions. For instance, developing software for civil engineers to calculate various parameters of any structure of buildings or software for aerospace. In summary, complex mathematical operations are used in various real-life programs and software, therefore, there is a need to know about them and their uses.
Interestingly, in Python, pieces of codes have already been created (that is what is known as libraries), for several mathematical functions. These codes can be used without any difficulties, and there is no need to rewrite them again. All that is needed is just some key information to be able to use them.
This can be described as a piece of code that may or may not take some value(s) as input, process it, and lastly may or may not return any value as output.
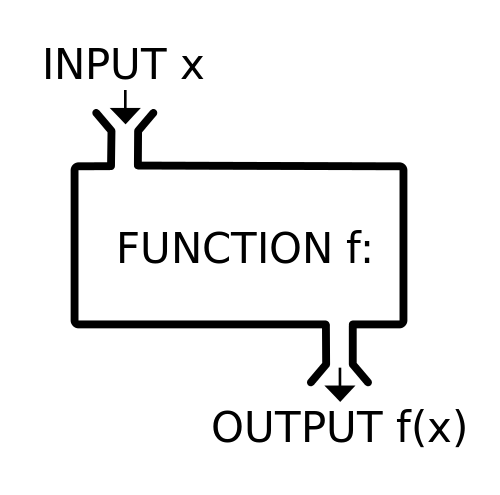
From the above figure, the input x is given to a function f and it is given some value f(x) as the output. However, in general, programming, depending on the purpose of the function, input, and output is completely optional, but a mathematical function needs both.
Now, for example, in the trigonometric function sin(x), there must be some value of x to calculate and return the answer, and this establishes the reason why math functions are both input and output.
There are two types of pre-defined functions in python.
Now let's check out some of these functions and how they are used in the mathematical operation.
We have done something like this in previous sessions of this tutorial, but, that one is an operator and was used to calculate power, but this one is an inbuilt function. It is an alternative way to calculate power. So, you do not need to import any other library file or modules for such calculation.
We already know that for power, the power function needs two numbers (i.e. inputs) to perform the operation; that is base and exponent, therefore we have to provide two numbers to the function. Check out the example below:
>>> pow(3,2)Now, after the python compiler has ensured that all the syntax is correct, it then looks for the implementation of the pow function and uses it to find 32. The output is shown below:

In the example above, we cleared up what function is. However, it can be generalized as:
>>> functionName(input1, optionalInput2, optionalInput3, ...)As said earlier. The values inside brackets which are separated by commas, as input to the functions, are called Arguments. That is, in the example of pow(x,y), 3 and 2 were the arguments. Also, we can have any other number of arguments in a function.
The Absolute function also referred to as Modulus, is different from Modulo. The Modulus returns the non-negative value of the argument value. As such, the absolute value of any non-negative number is the same, but in the case of negative numbers, their positive value is returned.
Syntax:
>>> abs(-99.99)Check out the example below:

Now let's try some functions where we have to import some modules(or library files).
You already know that sine is a trigonometric function, therefore it accepts just one value as an argument. For instance, x should be in radians, so should not mistake it with a degree. Note that we cannot use this function directly so that we will not get an error response; such as the one shown in the example below:

From the example above, the compiler doesn't know what it is supposed to do when it encounters the sin() function, because it was not defined and we tried using it. Therefore, for us to use it we have to import the Python math module, which consists of the implementation of the sin() function and it is what will guide the compiler to know what to do when it encounters the sin().
In the example below, what we want to do is known as importing a module and it can be done by using available ready-made functions. This is shown below.
>>> import mathPress the enter key, and that is it. So for us to use the sin() function, go to a new line and type this below:
>>> math.sin(3.14159)Since the value of π is approximately 3.14159, then the answer would be near zero.

In Python other functions available inside the math module, such as the floor() function, exp() (exponential function), log() (logarithmic function), and many more.
